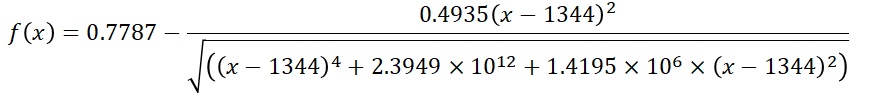「アルキメデスの大戦」見たよー !!ネタバレ注意!!

ちょっと久しぶりの更新になった。twitterに書くとネタバレになりそうなので、ひと目に触れにくいこっちに書いとく。

総論：面白い映画だった

結論として大変面白い映画だった。鑑賞前にtwitterで「理系にはたまらん」とか「因果推論やっててよかった」とか「実証分析屋のためにある映画だった」いう大変わかりみの強い感想を目にしていたので、期待して見たんだが、期待は裏切られることなく、たしかに面白い映画だった。

個人的には「逆問題の考え方結果から原因を探る数学 (ブルーバックス)」あたりを読んでおくとなお一層楽しめるのではないかと思った。

気になった点

ネタバレになるので、この先を読むのは鑑賞後にしたほうがいいと思う。なので、一応閉じておく。ただ間違って目に入ったとしてもなるべく固有名詞は出さないようにしたつもり。

この映画の最大の見せ所は、「詳細なデータがない中で、いかに限られた情報から特定の数値を推定するか」という点にある。当初、主人公はできる限りのデータ収集を行い、そこから演繹的に答えを推定しようとするが（当然、この方法も無謀なチャレンジであることは言うまでもない）、そもそものデータ収集にまずは機密という高い壁が立ちはだかり、さらに間接的なデータ収集にも敵方の妨害が加わり、演繹的な推計は遅々として進まない。さらにさらにタイムリミットの無情な繰り上げという敵方の卑怯な謀略が見事にはまり、主人公は絶体絶命な状況に直面する。

そこで主人公が起死回生の一手を放つのである。つまり、演繹的な数量×単価の積み上げによる推計ではなく、「過去の類似事例からの近似値の推計」という帰納的な手法への180度の大転換である。うーん、それ、僕も「なんちゃらの市場規模予測」とかで時間に追われて「まあこの市場の伸び率は大体この商品と似てるはずよね」とかやっちゃったことあります！（はにかみ）

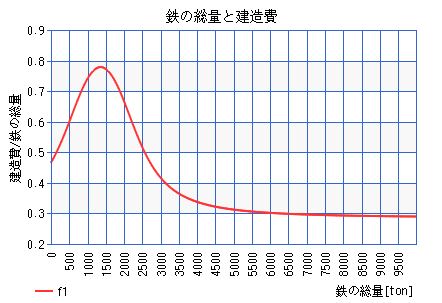
で、主人公は過去の様々なデータを二次元平面にプロットする。そしてyを「単位重量あたりコスト」とし、xを「その対象物の重量」としてかっこいい関数を導き出すのだ！はい！僕もExcelの近似曲線をR^2の高さだけで採用したことがあります！あと共線性とか考えずにSASでRandom Forestぶん回したりしたこともあります！（伏し目）

ちなみに、主人公の導き出したかっこいい関数はこんな感じ。

戦艦の鉄の総量と建造費の関係式（映画アルキメデスの大戦より） - 高精度計算サイト

そして、対決の場。主人公は自分が導き出したかっこいい関数の説明力を鮮やかに示してみせる。彼の導出した関数は実績値の完璧な再現力を持つスーパー、いやハイパー関数だったのだ！そして、そのハイパー関数に敵方の数字、それも操作の仕様のない数字を代入すると、見事、敵方の謀略が露見するのであった！押忍！僕もむかし「このマルチプルを当てはめれば先方の提示金額はかなり割高になっています。なんらかのDDの見落としか、評価の前提にミスリードな点があるのではないでしょうか？」とか適当なことを言ったことがあります！（恥じらい）

で、何が言いたいかというと、以下の２点です。

無理やり一つの関数で説明するんじゃなくて、元データを艦種ごとに分類して最小二乗法したほうがシンプルじゃね？
てか、そのかっこいいハイパー関数、オーバーフィッティング（過学習）じゃね？

以上です！

（画像に特段の意味はありません）

でもこの映画、設定といい役者のハマり具合といい、最後のオチといい、大変面白い映画なので、ぜひ劇場でご覧になることをおすすめします。